Proyecto Péndulo de Newton
PÉNDULO DE NEWTON
Jhan Matajira - Daniel Cárdenas - Silvia Flórez
VIDEO INTRODUCCION
RESUMEN
El péndulo de newton es un sistema que utiliza una
serie de péndulos iguales y que demuestran las leyes de conservación de momento
y energía, las cuales se derivan de las leyes de newton y establecen que en un
sistema aislado(cerrado), su movimiento lineal total del sistema se
conserva.
En este proyecto se estudiará y demostrará
experimentalmente este sistema de colisiones(Péndulo de Newton) según el caso
determinado, para las cuales se estudiará su momento lineal antes y después del
choque.
TEMAS
•
Momento Lineal
•
Conservación de energía
“El Péndulo de Newton está
basado en la ley de transferencia de energía. La naturaleza de esta teoría
describe como la energía no se crea o se destruye, sino que pasa de un cuerpo
físico a otro. El hecho de que el péndulo de Newton funcione
sin alimentación externa demuestra en parte esta teoría de la manera más
sencilla posible”.
https://www.ecured.cu/P%C3%A9ndulo_de_Newton.
DESCRIPCIÓN
Un conjunto de bolas de acero idénticas alineadas
cuelgas de hilos inextensibles. Al elevar una de las esferas de los extremos hasta
una altura dada y soltarla, ésta volverá a su posición original, golpeará a la
esfera siguiente y en contacto con el resto, y un instante después se observará
que la esfera del extremo opuesto ¡sale disparada! La segunda esfera seguirá
moviéndose en la dirección del golpe hasta llegar a una altura máxima, después
volverá a su lugar, provocando que esta vez salga disparada ¡la esfera
original!, aunque a una altura menor que al principio. Este proceso continuará
un rato, aunque se observará que después de cada golpe, la altura de las
esferas en movimiento será cada vez menor, hasta que se detenga por completo.
En caso de elevar y soltar dos de las esferas
simultáneamente, el movimiento será similar al anterior, sólo que en este caso
saldrán disparadas dos esferas en cada colisión. Lo mismo sucederá con tres o
cuatro esferas. Pero ¿cuál será la explicación de esta hipnótica experiencia?
OBJETIVO GENERAL
Comprobar la conservación de energía en la colisión (péndulo
de newton) Según el caso en específico.
OBJETIVOS ESPECIFICOS
•
Explicar de
manera sencilla por medio de la conservación de energía el funcionamiento del
péndulo de newton.
•
Medir las
velocidades iniciales y finales de cada uno de los cuerpos esféricos
involucrados en una colisión unidimensional (de un solo caso).
•
Calcular la energía cinética antes y después
del choque.
FUNCIONAMIENTO DEL PENDULO DE NEWTON
Al coger la primera bola y soltarla, la bola caerá y golpeará
la segunda bola, tratándose de un choque elástico, que a su vez golpeará a la
tercera bola y así sucesivamente hasta que la última bola sube y vuelve a caer
golpeando la anterior. En cada choque entre bola y bola se conserva la cantidad
de movimiento y momento, habiendo muy poca pérdida al no haber casi fricción ni
deformación de las bolas. Finalmente, el sistema acabará parando, ya que,
aunque la fricción es muy pequeña, si existe una pequeña fricción y por tanto
una pequeña pérdida de movimiento.
¿POR QUÉ FUNCIONA ASI EL PENDULO DE NEWTON?
Hay varios factores importantes que hace que el
péndulo de Newton se comporte de esta forma:
•
Las bolas en
el péndulo de Newton deben ser de la misma masa. Cualquier pequeña variación en
las masas provocaría otro comportamiento del péndulo.
•
No importa
cuantas bolas que se usen en el péndulo, sin embargo, cuantas mas bolas uses
más fácil será que haya desviaciones entre masas y al final que no funcione.
•
Las bolas
deberán estar perfectamente alineadas para la transmisión de la cantidad de
movimiento.
•
Se utilizan
bolas esféricas ya que el contacto entre ellas es prácticamente un punto. Se
podrían utilizar otra forma de objetos, pero esto podría provocar un
desalineamiento.
•
El material
del que están hechas las bolas, debe ser un metal duro, como acero inoxidable,
para evitar perdidas de energía en el choque.
•
Las bolas
deben colgarse con cuerda o alambre, manteniéndolas alineadas y minimizando de
esta forma las pérdidas debido a la fricción.
MARCO TEORICO
Para explicar de forma sencilla el experimento
asumiremos que las bolas no están inicialmente en contacto, por lo que las
colisiones se producen siempre entre dos bolas, y que son perfectamente
elásticas.
En primer
lugar, levantamos una de las bolas de los extremos hasta una cierta altura,
proporcionándole una energía potencial determinada,![]() . Al soltarla la bola se mueve a lo largo de un
arco de círculo hasta volver a su posición de equilibrio, cuando lo alcanza
toda su energía potencial se ha convertido en cinética.
. Al soltarla la bola se mueve a lo largo de un
arco de círculo hasta volver a su posición de equilibrio, cuando lo alcanza
toda su energía potencial se ha convertido en cinética.
En cuanto sobrepase dicha posición colisionará
con la bola vecina. Al tratarse de bolas de acero que no se deforman
permanentemente la colisión se podrá considerar como perfectamente elástica
conservándose energía y momento. Esto exige que todo el momento lineal y
energía se transfieran a la segunda bola que a su vez chocará con la tercera y
esta con la cuarta, etc.
De no existir disipación, una buena aproximación
en este caso, la última bola habrá adquirido la misma energía cinética que
tenía la primera y por tanto alcanzará una altura igual por el otro extremo a
la que le habíamos dado a la primera. La situación se resume en la figura.
Ilustración 3.Péndulo de
Newton. Caso 1. Fuente:https://www.ucm.es/data/cont/docs/76-2013-11-08-00_00_Newtons_cradle.pdf.
Si levantamos dos bolas en lugar de una en la parte
izquierda veremos como en la parte derecha se levantan también dos. Existen
muchas otras posibilidades.
Finalmente es posible asimismo convertir las colisiones en
inelásticas colocando algo de plastilina entre la primera bola y la segunda
bolas, en ese caso observamos que las bolas se mueven de forma muy distinta.
Al analizar una colisión en sí, por conservación del momento lineal y conservación de energía se tiene respectivamente que:
Estas ecuaciones pueden ser reescritas como:
Dividiendo (4)/(3), se obtiene que:
Reordenando podemos reconocer el coeficiente
de restitución, cuyo valor es 1 para un choque elástico
Si combinamos la ecuación (5) con la (1), es
posible obtener la velocidad final de cada cuerpo:
Ahora, llevando esto a nuestro caso, tenemos que todas las
masas son iguales y al analizar el choque entre dos conjuntos (de una o más
bolitas), uno se encuentra en reposo y el otro con velocidad v antes del choque. Luego, reemplazando en las
ecuaciones anteriores, el problema se simplifica a que justo después de la
colisión debe haber la misma cantidad de bolitas con cierta velocidad que las
que habían justo antes de esta. Cabe destacar que la relación entre la
velocidad y altura alcanzada por cada bolita se rige por simple conservación de
energía, en donde la energía cinética se transforma en potencial y viceversa:
LA ENERGÍA SE CONSERVA
Cuando un agente externo (por ejemplo, tu mano)
cambia de lugar a una de las esferas, ésta se modifica su posición con respecto
a la Tierra, provocando una ganancia en su energía potencial gravitacional. Al
soltar la esfera irá perdiendo altura, pero ganará velocidad hasta que llegue a
la parte más baja de su trayectoria, lo que significa que, al perder energía
potencial gravitacional, gana energía de movimiento o energía cinética. Ahora
podemos preguntarnos, ¿y qué pasa con la energía cinética de la esfera cuando
llega a su posición original?
Lo que sucede es que una parte de la energía de
movimiento se perderá en forma de sonido (por el choque con la esfera
contigua), aunque la mayor parte de la energía se irá transfiriendo de esfera a
esfera, hasta alcanzar la esfera del extremo opuesto, transfiriéndole
suficiente energía para ponerla en movimiento. Esta situación se repetirá,
desgastando poco a poco la energía del sistema hasta llevarlo al reposo.
Ahora sólo falta explicar por qué al jugar con más de
una esfera el movimiento se provoca en el mismo número de esferas con el que se
inició. Este cuestionamiento se puede explicar superficialmente, mencionando
que dependiendo de la masa del conjunto de esferas y de la velocidad que
adquieran antes de chocar con el resto, se transferirá una cierta cantidad
de movimiento, la cual se conservará a lo largo del movimiento. De modo que el
momento de dos esferas se transferirá a dos esferas en todo el trayecto
impulsando a dos esferas, y así sucesivamente. Y es precisamente esta causa la
que nos permite obtener efectos y sonidos interesantes cuando se pone en
movimiento simultáneo dos esferas en extremos opuestos, tal como se puede
observar en el siguiente video.
Ilustración 4. Ejemplo Péndulo de Newton https://www.youtube.com/watch?v=_eqCvvEkHeg.
METODOLOGIA
En este proyecto de investigación se llevarán a cabo
las siguientes fases metodológicas
•
En esta fase se tendrá en cuenta lo explicado durante
este proyecto, además de tener claras las variables
que influyen en el péndulo de Newton. Esto permite tener una relación entre el
modelo teórico que describe el fenómeno y la práctica experimental.
•
Se procederá a realizar el experimento casero guiado
del video: “Péndulo de Newton casero (experimentos en casa) “. Luego se realizarán
2 casos específicos con Tracker para este proyecto. El video con el cual se construyó
el péndulo fue:
Ilustración 5. Experimento Péndulo. Sacado de: https://www.youtube.com/watch?v=1apTRvE-8cg&t=267s.
•
se debe realizar el montaje experimental que se
muestra anteriormente. En donde se ubicará el celular en algún lugar que
permita que este permanezca quieto.
MATERIALES
1.
Cámara.
2.
5 canicas del mismo tamaño(2.5cm) y masa.
3.
2 soportes de aluminio.
4.
3 vidrios de medidas (10x14)cm, (12x23)cm, (10x23)cm.
5.
Hilo o cuerda.
6.
Silicona liquida (especial para vidrio).
7.
Tijeras, regla, etc.
Usando la cámara se tomarán
2 videos. El primero será el caso de levantamiento de una canica y el segundo
del levantamiento de 2 canicas.
•
Por último se realizarán las mediciones pertinentes y se
medirá la masa, la velocidad y la energía tanto cinética como potencial de las
canicas antes y después del choque, para cada uno de los videos.
MEDICIÓN DE MASA
Por medio de una balanza
digital se medirá la masa de cada canica, mostrada en la siguiente ilustración.
Ilustración 6.Medición masa.
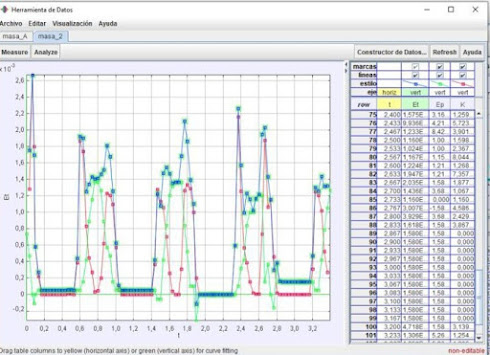
MEDICIÓN DE LA VELOCIDAD
utilizando Tracker se van a registrar las
posiciones antes y después de la colisión de cada una de las canicas, para los
videos que se grabaron. Después de capturar los datos se procede a usar el
mismo software para mostrar las gráficas de 𝒙 vs 𝒕 para cada una de
las canicas en los momentos antes y después de la colisión. Con cada una de las
gráficas, se debe encontrar la pendiente de la recta mediante el ajuste de los
datos, está pendiente corresponde a la velocidad del objeto respectivo.
MEDICIÓN DE ENERGIA CINETICA Y POTENCIAL
en esta última se deben calcular las energías
antes y después de las colisiones, para cada caso registrado en los videos. Con
ello se sintetizarán los resultados obtenidos en un análisis de datos y
conclusiones que se presentarán al final de este proyecto.
TRATAMIENTO DE METODOLOGIA
PARA MASA 2
PARA MASA 3
PARA MASA 4
PARA MASA 5

VIDEO CASO 2 CANICAS LEVANTADAS
(aclaramos que para usar la aplicación se uso un intervalo de tiempo del video no mayor a 1 seg)
PARA MASA 1
PARA M2
PARA M3
PARA M4
PARA M5
ANALISIS Y CONCLUSIONES
Análisis para el segundo video (Se hace prueba con dos canicas)
A raíz de los resultados obtenidos de los videos por la simulación hecha
en tracker se pueden comparar los números deseados evidenciados en la teoría
,lo que se ha de esperar es que la
energía del sistema se conserve, o por lo menos en un numero muy similar, dado
que en la practica hay bastantes factores los cuales afectan a los resultados
finales, encontramos una fuerza gravitatoria y además cierto tipos de
rozamientos, además se ha de aclarar que las cuerdas que sostienen las canicas
no son cuerdas ideales, teniendo esto en cuenta miramos los resultados
obtenidos en esta práctica:
PARA M1 PARA M2
Es de aclarar que ambas canicas son soltadas al
mismo tiempo, movidas por la misma fuerza que genera su aceleración, solo que
una esta un poco más arriba que la otra, esto explica, la variación en la
energía, pues la masa uno oscila entre 2,8 J, y -0,2 J, los valores negativos
se explican por que se evidencia el momento en la cual esta choca sobre la otra
canica y transfiere su energía, la masa dos por su parte oscila también entre
valores entre 2,6 J y 0 J, como se observa la varianza entre las dos canicas en
mínima, estos mismo números o algunos muy cercanos a estos son los
PARA M3
La canica tres, no presenta movimiento, pues
esta solo transfiere la energía, sin embargo, presenta por su altura energía
potencial.
PARA M4 PARA M5
Al observar los valores de las energías en las canicas 4 y 5 se evidencia que los valores de energía se transfirieron de manera precisa y los resultados de este experimento son los esperados, ya que aunque la transferencia de energía no fue del cien porciento sin embargo estos valores son muy parecidos a los iniciales en las canicas 1 y 2, pues oscilan entre 3.2 J y 0 J al igual que en la otra canica que oscilan entre 2,4 J y 0 J, observamos que hay un pico de energía máxima en la canica 4, esto puede ser producido por un factor externo, ocurrido por que el sistema no esta aislado, sin embargo no afecta mucho a los resultados dado que la variación en ambas energías es prácticamente la misma.
Análisis primer video (Una sola canica)
 |
|||
MASA 1  MASA 2 |
|||
MASA 3

MASA 4
MASA 5
En este segundo ejercicio, solo tira una
canica y por lo tanto esto solo hace que se mueva la última canica, por ende,
las energías tanto de la primera canica como de la última deben ser muy
similares, y las otras tres canicas sin presentar alteraciones en sus energías
durante ese momento ya que funcionan como puente entre las energías de las
canicas.
La energía de la primera canica oscila entre los valores de 3,2 J y 0 J,
mientras que los valores de la energía de la ultima canica oscilan entre 3 J y
-.0,2 J sin embargo esta ultima canica presenta un punto de energía máxima en
4,2 J, esto debió ser provocado por factores externos que afectan al
experimento, sin embargo la mayoría de los resultados son los esperados, con
una variación mínima de la energía, por ende vemos que el péndulo de
newton mostrado en este experimento
cumple con las expectativas teóricas esperadas.
Conclusiones:
·
La
construcción del péndulo se debe efectuar de la manera más exacta posible,
asegurándose de que las masas pesen lo mismo y las longitudes de las cuerdas
sean equivalentes para asegurar unos resultados acertados a los esperados
·
El numero
de canicas que impactan con la o las canicas puente son las que se les
transfiere esta energía, por ende, si lanzamos tres canicas, tras canicas
tendrán la energía de estas, si lanzamos dos solo se les transferirá energía a
esas dos ultimas canicas.
·
La energía
presenta variaciones, pues no es exactamente la misma cantidad que se
transfiere a las canicas en ninguno de los experimentos realizados, esto debido
a que el sistema no esta aislado y presentan puede presentar alteraciones por
factores externos
·
Las
canicas que funcionan como puente para la energía solo presentan energía
potencial, en todos los momentos de la transferencia de energía.
Bibliografia
https://www.ucm.es/data/cont/docs/76-2013-11-08-00_00_Newtons_cradle.pdf.
https://experimentosfisicauc.wixsite.com/experimentos/pendulonewton.
https://www.youtube.com/watch?v=1apTRvE-8cg&t=267s.

























Thanks for nice information
ResponderEliminarFastabiqul Khairat